Har varit borta ett par dagar, trodde nu att jag skulle få läsa här om en verifierat 20 dBi Yagi, tog det stopp?
Läser gärna mer. Ursäkta om jag sölar ner tråden med detta inlägg, men det hänger lite lösa trådar som jag vill kommentera.
jonasolof skrev:Intressant om Fresnelzonens storlek i förhållande till gain. På de websidor jag sett där Fresnelzonens storlek kan beräknas har den enda variabeln varit frekvensen. Det torde då innebära att man utgår från en 0 dB antenn.
Ökar Fresnelzonens storlek med gain på det tjockaste stället och i så fall hur mycket? Finns det en given relatíon till gain?
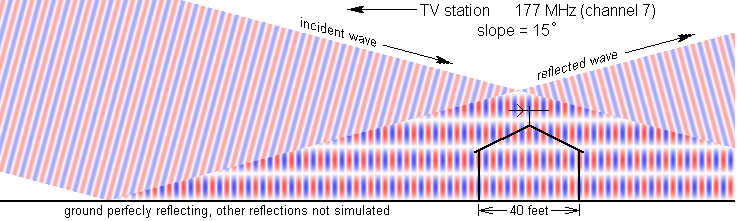
Jag valde en något olycklig bild för illustration, bara nappade något, som visar 1:a Fresnel zonen, vilken är relaterad till våglängd och överföringsavstånd.
Min formulering i samma text är missledande. Skulle i sammanhanget ha skiljt på några begrepp.
Citerar mej själv från tidigare inlägg:"Fresnel-zon av betydelse för antennen växer i proportion till gainet". Fresnel-zonen i sej är bara en måttstock som inte påverkar gainet. Det skulle hellre stått "Fresnel-region" men avstod då skillnaden zon och region är komplicerat med långrandiga förklaringar, men vi gör ett mindre försök.
Fresnelregionen i antennens närområde växer med ökat gain och för en given apertur i närfältet ökar antennens förluster.
Ökade förluster i antennens närfält kostar uppmätt antenngain om antennen mäts under dessa omständigheter.
Detta till skillnad från förluster i fjärrfältet, vilket inte påverkar antennens gain.
Om närfältsförlusterna sedan ska kallas förlust eller enbart nöja sej med att kalla det för reducerat antenngain beror på vilket närområde det gäller samt om man anser att antennens gain är det resultat man får när antennen mäts i fri rymd, eller betraktar en vind med vindsfönster som en del av det totala, vilket det är om störningen är i antennens närområde.
För att ta en jämförelse så påverkar två Yagi-antenner varandras gain om de placeras i samma närfält men inte om de finns i varandras fjärrfält.
Hurdan denna förlust ser ut beror på om det som påverkar antennen är absorbtion eller reflektion samt avståndet till antennen, vilket brukar delas in i regioner.
Reflexer och aperturer (typ ett vindsfönster) kan ge upphov till olika typer av diffraktion medans absorbtion inte ger detta fenomen, men i stället kan ge skuggeffekter. Påverkan beror även på avståndet till antennens olika nätområden i förhållande till hindret.
Regionen närmast antennen kallas Kirchhoff eller reaktiva regionen, sedan Fresnel som följs av Huygens och fjärrfältet, Fraunhofer.
Det som utmärker Fresnel-regionen är att ett visst EM-fält har utvecklats men det är ännu inte en plan våg.
Det är ofta i denna region som triviala föremål kan ge stark påverkan på antennens egenskaper.
Förändrat strålningsmönster och påverkan av antennens impedans är vanligt. Bägge påverkar gainet dels genom återkoppling till antennen, dels som diffraktion vilket avspeglas även i fjärrfältet.
Fresenel-regionens grad av storlek brukar beskrivas som en kombination av antennens fysiska storlek och antenngain. För en Yagi, i strålningfältets huvud-utsträckning har även närfältet en större utsträckning.
Aperturens påverkan beror på storleken, medans vilken formel man ska använda för beräkningen styrs av vilken region man befinner sej i.
I det aktuella fallet antas att vindsfönstret är i Frenel-regionen,dess inverkan på diffraktionsförluster kallas Fresnel-nummer. Högt nummer ger lägre förluster.
Fresnel-nummer har inte något med siffran som markerar olika lager av Fresnel-zoner i fjärrfältet.
Detta nummer är ett tal större än 1 i Fresnel-regionen. Om talet är mindre än 1 är det per definition ett Frauenhof-nummer.
Numret kan alltså även användas för att beräkna vilken region aperturen befinner sej i.
Enklare tumregel är att Fresnel-regionen finns i området 0,1-10 våglängder framför en Yagi-antenn med 10 dBi gain. Bortanför 10 våglängder finns fjärrfältet.
En dipols fjärrfält är betydligt närmare antennen. Redan vid tre våglängder är vågutbredningen hyggligt plan.
Sambandet mellan detta Fresnelnummer och antennens gain är komplicerat även om antennens egna apertur är inblandad, men det finns en formel som är enkel i sammanhanget gällande vindsfönster-aperturen.
N: Fresnel-nummer
a: aperturens radie (liten radie kan ge antennförlust pga deformerad vågutbredning, diffraktion, för önskad riktning)
D: överföringsavstånd
L: våglängd
N*D*L≡a*a
Om frekvens och överföringavstånd är konstant i denna formel, är aperturradien kvadratiskt relaterat till Fresnel-nummret.
Om antennaperturns radie är konstant, blir Fresnel-numret i proportion till våglängd och överföringsavstånd.
Observera likheten med hur 1:a Fresnel-zonens storlek enligt tidigare bild beskrivs som relaterat till våglängd och överföringsavstånd.
Formlen är allt för ofullständig för att vara användbar för ett praktiskt fall, för en punktformig ljuskälla är det något enklare men här kommer vågrörelser med många olika vinklar och faser från de olika Yagi-elementen, det är alltså inte lönt att försöka göra kalkyler ännu.
Vill man fördjupa sej är det nog enklare att börja med att se på de ideala fall som beskrivs på nätet, relaterade till Fraunhofer-nummer.
En viktig skillnad reltivt Fresnel-regionen är att apertur-relaterade förluster för Fraunhofer-regionen påverkar sträckförlusten, påverkar således inte antenn-gain.
Det är i Fraunhofer-regionen, fjärrfältet, som man som till en regel har diffraktion pga av t.ex. byggnader eller bilar.
För Kirchhoff-regionen finnns inga nummer eftersom det inte finns någon utvecklad EM-våg i denna region.
Fresnel, liksom andra omnämnda gubbar, sysslade med optik, men som det mesta inom vågrörelselära för radiovågor har teorier omplanterats från optikens värld och vid behov har uttryck justerats något. Vågutbredning inom optiken beskrivs oftast enligt Huygens-Fresnels princip som överlagring av sfäriska vågor som uppstår från punktkällor. Detta till skillnad för EM-vågor där fjärrfältet beskriver vågutbredningen som en överlagring av plana vågor som utbreder sig i olika riktningar genom rummet. vinkel-spektrumet av en våg blir dess tvådimensionella fouriertransform.
http://en.wikipedia.org/wiki/Huygens%E2 … _principle
Fresnel nummer ur optiskt perspektiv: http://en.wikipedia.org/wiki/Fresnel_number
I fjärrfältet.
A. Som till en regel är öppningsvinkeln för antennen betydligt bredare än bredden på aperturarean, vilket gör att mätbar diffraktion kan ske över ett brett område (många Fresnel-zoner).
B. Om ett helt tvärsnitt av 1:a Fresnel-zonen är blockerad av något med 100% absorbtion kommer viss del RF-signal att runda hindret pga av skuggeffekt och troligen även pga diffraktion. Signalen blir dämpad men inte totalt.
Man kan jämföra skuggeffekten med att om man sätter upp en 100% dämpande ljudskärm utomhus på ett relativt reflexfritt område, kommer ljudvågor att vinkla av när de rundat hindret. En bil som väsnas på den ena sidan kommer fortfarande delvis att höras på andra sidan, om inte skärmen är oändligt stor.
Samma sak gäller vattenvågor, medans effekten är betydligt mindre för ljusvågor och för ännu högre frekvenser, partikelvågor finns inte skuggeffekten om man inte blandar in krafter såsom gravitation. Denna skillnad är en av anledningarna till att man inte alltid rakt av kan låna formler från en typ av vågrörelse till en annan.
Kvantmekanisk vågrörele-lära delar inte denna uppfattning, de håller sej till en enda formel oavsett våg-typ.
Det mesta av vågrörelse-teorierna härrör från optikens värld. Söker man information om vågrörelser på nätet så är 9 av 10 träffar om optik. Tror det historiskt har med att göra att det är ett fenomen som kan betraktas med ögonen och därmed enklare att verifiera teorier.
En sammanfattning:
1. Resulterande antenngainet är relaterad till Fresnel-regionen och kan påverkas negativt eller positivt för något som uppstår i relativt närfält. Hit räknas i detta fallet t.ex. fönsterkarmar på någon meters avstånd även om t.ex. loben i fjärrfältet är smalstrålande och antyder att loben "går fri" genom ett befintligt fönster.
2. Antennens gain påverkas ej av hinder eller reflektioner som finns i antennens fjärrfält (Fraunhofer-regionen eller distanta Fresnel-zoner). Där är det sträckförlusten, vilken utgörs av rymdämpning (Friis ekv.) och fysiska hinder som kan ge upphov till absorbtion, reflektion och dess Fraunhofer-diffraktion (ej att förväxla med Fresnel-diffr).
3. Antennens strålningsdiagram sett i fjärrfältet, är kraftigt deformerat i närfältet, så man kan få ett mycket annorlunda resultat om man t.ex. mäter fältstyrka i närfält resp. fjärrfält och det är en glidande övergång. Därför blir t.ex. verkliga beräkningar av närfälts-aperturer, antennens egen eller i omgivningen, mycket komplexa. Tar man med det faktum att EM-vågen inte har en rätlinjig front i denna region blir det än stökiga beräkningar.
4. Denna text är ofullständig i sitt innehåll, det är bara lite skrap på ytan om vågrörelse-lära som i stort sett bara skrivs ner direkt ur huvudet och i bästa fall blir det en snabb korrekturläsning. Kolla med fristående källor innan det satsas eller inte satsas på stora antennbyggen baserat på mina påståenden.
En pedagogisk Youtube-film om aperturer i fjärrfält: https://www.youtube.com/watch?v=BH0NfVUTWG4
---
Kommentar på tidigare funderingar.
Jämförde tidigare antenngain med reflektor på parabol, där större reflektor oftast ger högre gain. Men det är inte någon nödvändighet att antennen ska ha stor fysisk tvärsnitts-area för att få högre gain eller större aperturarea.
För en Yagi-antenn, kort som lång så har den ungefär samma fysiska tvärsnitts-area trots olika gain.
Enkel förklaring varför en Yagi-antenn trots begränsad fysisk tvärsnitts-area ändå skapar en stor apertur-area är att samtliga element i en Yagi-antenn samverkar som om de vore stackade dipoler, även om ingen kabelförbindelse finns mellan elementen. Detta bygger på effekter som specifikt uppstår i Fresnel-regionen men mäts alltid i Fraunhofer-regionen. Jämför även med en logperiodisk antenn, där varje element är fysiskt kopplade via gemensam transmissionsledning.
Slutligen så är det fel att kalla större Yagi-antenner för Yagi-antenner. Antenn-typen heter Yagi-Uda efter dess bägge upphovsmän, professor Yagi och hans assistent Uda, där Uda tillskrivs som den egentliga upphovsmakaren, ca 1923?.
Även jag skriver Yagi-antenn, trots att jag kanske borde veta bättre, slarvar med Fresnel-zon när jag borde skriva Fresnel-region osv. Kan nog hända igen.